回溯
回溯法是一个万金油算法,它的本质是优化了的暴力搜索,其基本思想是 深度优先搜索 以及 剪枝 ,适用于求解 任意解 ,所有解 或 最优解(可能不是最好的方式) 的场景,后两者都需要探索整个解空间。
1. 基本思想
- 每一步的 选择 和 问题状态的变迁 构成了一棵 解空间树 ,可以看作每个节点都存储着这两种信息。
- 用 深度优先 的方式遍历这棵树,当到达 目标状态 时停止,此时从根节点出发的路径即为问题的一个解。探索过程中,若当前节点的子树可能有解则继续往下探索;若无解则回溯。
- 剪枝:判断当前节点的子树中是否有解的函数称为 剪枝函数,很形象的,‘剪掉子树’。主要有
可行性剪枝 [状态是否合法]最优解剪枝 [求最优解时]状态判重剪枝 [状态可能重复时]。
2. 实现与模板
现在来考虑实现,一般的,我们需要:
一个stack保存当前的遍历路径(每一步的选择),随着探索不停的push和pop元素;
当完整解的高度固定时,可以用一个数组 + 栈顶索引index,来模拟stack。注意,初始栈为空,index初值为-1。
一些变量保存问题的 状态,在探索和回溯过程中不停地改变和恢复:
比如,假设当前探索到节点P,此时的状态是S(P),往下探索时,假设它有两个孩子节点C1和C2。首先考虑C1:
// 伪代码 stack.push(C1) 状态 = S(C1)当 a. C1被剪枝了;b.C1的子树都被探索完时,我们该考虑C2了。在对C2进行上述两步之前,需要
恢复状态到父节点并出栈C1,第一步很容易遗漏:// 伪代码 状态 = S(P) //!记得恢复状态 stack.pop() // 此时考虑C2 stack.push(C2) 状态 = S(C2)需要注意的是,很多问题中(如八皇后/数独),stack中保存的部分解就可以表达当前问题的状态,此时就没有必要专门去跟踪了。
函数
isComplete(),判断当前是否找到了 完整解。通常根据 是否到达目标状态,当前路径的长度 判断。
剪枝函数
isPartial(),判断当前stack 是不是一个合法的 部分解。判断有没有必要继续向下探索。
当探索到达树的底部,还需要判断当前是不是合法的 完整解。
给出用回溯法(递归的方式)求 全部解 的模板如下:
// 探索时存放路径,即部分解。当树的高度确定时,可用index+array代替栈,index是stack的栈顶位置, 其初始值为-1.
var path = new Stack()
// 状态随节点转移而改变。注意,很多情况下status可以由path来表达(比如N皇后/数独,棋盘的状态就存放在path中),这时就省去了状态转移的这个步骤了。
var status = init status
// 其含义其实是对当前栈顶节点的子树进行探索
function explore(){
// 找到一个完整解
if(isComplete()){
print path
return;
}
for(choice : choices of last node(eg. P) in path){ // 这里可以做一个优化:更优的选择先探索
path.push(choice)
transform status // P转移到choice节点的状态计算
// 剪枝
if(isPatial()){
// 剪枝失败,进入choice的子树探索
explore()
}
// 剪枝成功或choice的子树探索完毕,探索P的下一个子节点。
restore status // --> 不要忘了状态的恢复!
path.pop()
}
}
// 根据path或status判断是否找到了完整解
function isComplete(){
}
// 剪枝
function isPatial(){
// 对于path中存放的部分解进行 *可行性剪枝*,即判断status是否合法/后续探索是否有可能找到一个完整解
}
// 调用
explore()只需保存路径,空间复杂度为O(height of tree)。
3. 实例
3.1 八皇后
应用回溯法时,最重要的有两点:
- 问题的状态 是什么(什么信息需要跟踪),初始状态 和 目标状态 各是什么;
- 如何明确定义解,即 如何一步一步进行探索。同一个问题,解的表达方式可能有多种,某些形式可能更容易处理,如更少的探索次数、更易剪枝、可以在搜索过程中避免状态重复等,要多利用解的特点;
以八皇后为例,一种直接的探索方式为:
// --解的表示方式
使用一个长度为n的数组保存每个皇后在棋盘中的坐标(取值范围0..n^2);
// 探索过程
对第1个皇后,可以放在棋盘的任意位置(n^2种选择);固定皇后1后,皇后2可以选皇后1以外的位置;同样的,皇后3可以选择皇后1/2之外的位置;...以此类推,每次选定位置后利用规则进行剪枝。这种探索方式的缺点有两点:
- 平均每次探索的选择都是O(n^2)的,待选节点规模太大;
- 会出现重复状态(如皇后1选择[0][0],2选择[0][1];vs 1选择[0][1],2选择[0][0],这两者所到达的棋盘状态是一样的),需要额外的空间和时间进行状态保存和判重。
仔细考虑解的特点,最后的解必然会在每一行上有且仅有一个棋子,因此可以用下面的探索方式:
// --解的表示方式
使用一个长度为n的数组,每个元素代表该行上皇后所在的列(取值范围0..n);
// 探索过程
对第1个行,皇后可以放在该行的任意位置(n种选择);对第2行,同理;...以此类推。可以看到,上面的方法避免了前一种的两个问题:子节点的规模为O(n),且不会出现重复状态。代码如下,和模板基本上是一一对应的:
#!/usr/bin/python
# coding=utf-8
import math
class Solution:
def solveNQueens(self, n):
self.n = n
# 栈(数组)和栈顶,保存每一行上皇后所在的列
self.stack = [None] * n
self.stackTop = -1
# 不需要额外记录问题的状态,路径就可以表达棋盘的状态了
self.explore()
def explore(self):
# isComplete():
# 探索完了最后一层,即栈指针指向最后一个元素。此时stack中保存一个完整解。
if self.stackTop == self.n - 1:
print self.stack
return
for i in range(0,self.n): #每一层有n个选择
# push
self.stackTop += 1
self.stack[self.stackTop] = i
# 剪枝 & 继续探索
if self.isPatial():
self.explore()
# pop
self.stack[self.stackTop] = None
self.stackTop -= 1
def isPatial(self):
# 可行性剪枝:
# 两个皇后不能在一行/一列/一条斜线
# 这里利用了一个特性:
# stack中[0..stackTop - 1]的排列方式可以保证已经是符合规则的,只需要考察stackTop和之前的每个皇后是否满足规则即可。
lastCol = self.stack[self.stackTop]
i = self.stackTop - 1
while i >= 0:
col = self.stack[i]
if lastCol == col or math.fabs(self.stackTop - i) == math.fabs(lastCol - col):
return False
i -= 1
return True
if __name__ == "__main__":
Solution().solveNQueens(6)
# [1, 3, 5, 0, 2, 4]
# [2, 5, 1, 4, 0, 3]
# [3, 0, 4, 1, 5, 2]
# [4, 2, 0, 5, 3, 1]4. 求任意解
如果只要求一个解,可以用一个变量维护当前解是否找到,每次探索完了先看一下,如果已经找到了解就立刻返回。
solutionFound = False # 1
def explore():
if isComplete():
solutionFound = True # 2
return
for every step in Steps:
...
if isPatial():
explore()
if solutionFound: # 3
return
...
5. 求最优解
思路:
- 维护当前找到的最优(完整)解及其对应的状态;
- 剪枝时,除
可行性剪枝,还需要进行最优解剪枝:如果当前的部分解比已知最优解还差,就可以停止往下探索了; 最优解剪枝会淘汰掉比已知最优解差的”完整解”,因此当确实找到了一个完整解时,即为新的最优解;
因此,在实现中需要增加的逻辑有:
... // stack/status
// 已知最优解及其状态 ---- 改动1
var bestSolution = None;
var bestStatus = None;
function explore(){
// 找到一个完整解,即新的最优解
if(isComplete()){
// 更新已知最优解及其状态 ---- 改动2
bestSolution = stack.copy();
bestStatus = status;
return;
}
for(choice : choices of last node(eg. P) in path){
...
// 注意,即使choice已经到达最后一层且组成了一个合法的完整解,如果不是当前最优的,也会被剪掉。
}
}
// 剪枝
function isPatial(){
// 1. 可行性剪枝
// 2. 最优解剪枝 ---- 改动3
}
explore()
// 算法结束后,bestSolution就是最优解了。5.1 01背包
01背包属于下面提到的“子集树”的情况,为了搜索,使用一个长度为n的数组作为探索时的栈,每个元素只有两种可能取值,0-不选,1-选。问题的状态由 当前物品的总价值 以及 当前物品的总空间 二者表达,在遍历时需要维护这两个状态。虽然他们可以由stack中的元素计算而得,但耗时O(n);
为了求最优解,还需要跟踪当前最优解及其对应的问题的状态;
最后,如何利用最优解进行剪枝? 假设考察k,物品[0..k-1]已经确定了是否选择,如果[0..k-1]得到的总价值,再加上剩余所有物品的价值总和,依然小于当前最优解,则可以放弃探索了。
代码实现如下:
#!/usr/bin/python
# coding=utf-8
# 0/1背包问题
v = [8, 9, 10, 4, 1, 15] # 物品价值
c = [2, 1, 5, 3, 3, 7] # 物品空间
n = len(v) # 物品个数
bag = 12 # 包的总空间
# DFS需要的信息
stack = [None] * n # stack
stackTop = -1
totalValue = 0 # 问题的状态 -- 1. 所选物品的总价值,初始没选物品,为0;
totalCapacity = 0 # 2.所有物品的总空间
# 其实由path中也可计算得到,但是耗时O(n).
# 求最优解需要的额外信息
bestSolution = None # 当前最优解
maxValueFound = None # 最优解时的物品总价值
def explore():
global stackTop,totalValue,bestSolution,maxValueFound,totalCapacity
# 找到了新的最优(完整)解
if stackTop == n - 1:
bestSolution = stack[:]
maxValueFound = totalValue
return
for i in range(0,2): # 子集树
# push
stackTop += 1
stack[stackTop] = i
# transform status
totalValue += v[stackTop] * i
totalCapacity += c[stackTop] * i
if isPartial():
explore()
# restore status
totalValue -= v[stackTop] * i
totalCapacity -= c[stackTop] * i
# pop
stack[stackTop] = None
stackTop -= 1
def isPartial():
# 1. 可行性剪枝
if totalCapacity > bag: # 占用空间超过袋子的总空间,则不合法
return False
# 2. 最优解剪枝
if maxValueFound != None: # 已经找到了一个最优解才进行最优解剪枝
# 剪枝的依据:如果当前获得的物品价值(totalValue),加上剩余所有物品的价值,依然小于当前最优解,则剪掉
c = totalValue
for i in range(stackTop + 1,n):
c += v[i]
if c < maxValueFound:
return False
return True
if __name__ == "__main__":
explore()
print bestSolution,maxValueFound6. 排列树和子集树
给定一个集合和提问,有两种特殊的情况:
6.1 子集树
从集合中挑一个满足条件的子集,解是[0,1,0,0,1]的形式,表示各个元素是否选择,解空间规模为 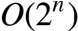
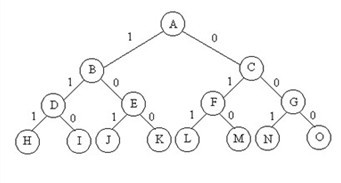
子集树的处理与之前一致,每次探索只有两个选择,0和1:
// old
for(choice : choices of last node(eg. P) in path){
...
}
// new
for(i = 0;i<=1;i++){
...
}6.2 排列树
求集合的满足条件的某种排列形式,解空间规模 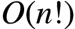
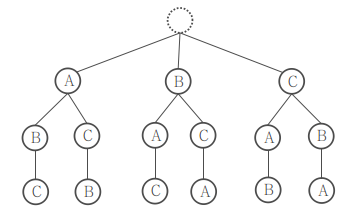
每次探索都只能选择之前没出现过的元素,这个限制可以用一个简单的方式实现:
- 保存探索路径的 stack 和 原始元素的集合 共用同一个数组;
- 假设0..k-1是已经确定了的探索路径(即 stack),在考察k时,则可以选k..n之间的每个元素;
- 对栈的 push 和 pop 可以用两次 swap 搞定
// old
for(choice : choices of last node(eg. P) in path){
...
}
// new
// [0..stackTop]已经确定,对stackTop+1考察,可选元素为 [stackTop+1 .. n-1]
for(i in [stackTop+1 .. n-1]){
// push a[i] to stack
swap(++stackTop,i);
// transform status...
// 剪枝或继续探索
// restore status...
// pop
swap(i,stackTop--);
}用两个swap也可以达到同样的效果且更简洁,但不太好理解。
排列树 和 子集树 是很常见的两类问题,且都不会出现重复状态,属于比较简单的情况,一定要好好理解。
7. 状态记录和判重
在稍微复杂的问题中,经常会出现状态重复的情况,即经过若干步探索后到达了一个之前已经探索过的状态,这种情况在讨论八皇后问题时已经看到过了。
通常用hashset保存所有已经访问过的状态,并且利用它们进行剪枝。当求最优解时,不仅要保存状态,还要保存到达该状态的路径的某些信息如长度;进行状态重复剪枝时,当状态重复但 当前的部分解 优于 记录的部分解 时,是不能剪枝的。
代码的改动有:
... // stack/status...
function explore(){
// 记录已经访问过的状态,在此处进行可以保证初始状态和最终状态都被记录
recordStatus(); // <---- 1
if(isComplete()){
...
}
var statuses = new HashSet/HashMap() // 所有已经访问过的状态 <---- 2
function recordStatus(){
statuses.put(curStatus); // 如果状态复杂,可以拼接出一个String表示
}
// 剪枝
function isPatial(){
// 可行性剪枝
// [最优解剪枝]
...
// 状态重复剪枝 <---- 3
}7.1 传教士和野人问题
题目如下:
有P个牧师和C个野人过河,只有一条能装下两个人的船,在河的任何一方或者船上,如果野人的人数大于牧师的人数,那么牧师就会有危险. 你能不能找出一种安全的渡河方法呢(P>=C)?
由于是求任意一个解,因此按照回溯法的思路分析如下:
- 很明显,解空间树的高度是不确定的,不能用数组+索引当stack用,需要一个动态的栈;
问题的状态由什么表达?
左岸牧师人数 + 左岸野人人数 + 船的位置
初始状态和目标状态是什么?
初始:左岸P个牧师,C个野人,船在左边;目标:全部牧师和野人、船都在右岸
每一步有哪些选择?
这里每一次探索的选项是固定的:运送2p/1p/1p1c/1c/2c,5个选择
哪些可行性约束?
显然的,两岸的野人和牧师都不能是负数;此外,当有牧师存在时,牧师不能少于野人
但是,这个问题显然是会出现重复状态的。举个例子,假设第一步送两个牧师到对岸,第二步也选择送两个牧师,这样状态就和初始状态一模一样了;即很有可能经过n步搜索后发现到达了一个曾经到过的状态。因此,为了防止无限的搜索,必须在搜索的过程中记录当前状态并以此剪枝。
代码如下:
#!/usr/bin/python
# coding=utf-8
# 4种选择
class Step():
def __init__(self,p,c):
self.p = p
self.c = c
def __str__(self):
return 'Pastor: ' + str(self.p) + ' Cannibal: '+ str(self.c)
Step.all = [Step(1,1),Step(1,0),Step(0,1),Step(2,0),Step(0,2)]
totalP = 3 # 总牧师
totalC = 3 # 总野人
# DFS需要的信息
stack = [] # stack
p = totalP # 问题的状态。 p:左岸的牧师,c:左岸的野人,boat:船在哪边(为了方便计算,在左岸时-1,右岸时1)
c = totalC
boat = -1
# 第一个找到的完整解
aSolution = None
def explore():
global aSolution,p,c,boat
# 记录当前到达的状态
recordStatus()
# 如果找到了解,返回
if aSolution != None:
return
# 根据目标状态判断是否找到了完整解
if p == 0 and c == 0 and boat == 1:
aSolution = stack[:]
return
for step in Step.all:
# push & 状态转移
stack.append(step)
p += boat * step.p
c += boat * step.c
boat = -boat
if isPartial():
explore()
# 状态恢复 & pop
p += boat * step.p
c += boat * step.c
boat = - boat
stack.pop()
# 状态记录相关
statuses = {}
def recordStatus():
statuses[curStatus()] = True
def curStatus():
return str(p) + "_" + str(c) + "_" + str(boat) # 当前状态:"左岸牧师_左岸传教士_船的位置"
def isPartial():
# 1. 可行性剪枝:
# a. 两岸的牧师和野人不可<0
# b. 两岸当有牧师时,牧师不得少于野人
if p < 0 or c < 0 \
or totalP - p < 0 or totalC < 0 \
or (p < c and p > 0) \
or (totalP - p < totalC - c and totalP - p > 0):
return False
# 2. 状态判重剪枝
if curStatus() in statuses:
return False
return True
if __name__ == "__main__":
explore()
if aSolution == None:
print "no solution"
else:
print [str(s) for s in aSolution]如果是求步骤数最少的方案呢?