几个常见的概率问题

几个常见的概率问题

今天研究了下几个简单的概率问题，在这里记录下。

1. 洗牌

问题很简单，有 n 个元素，设计一个能保证随机性的洗牌算法。

直觉想到的算法是：

用一个数组作为新牌堆，不停地从原数组剩下的元素中随机挑一个放入新牌堆，直到原牌堆耗尽。

我们来验证一下它的随机性。考虑一个元素，洗牌后它在第一个位置（即第一次抽牌就选中它）的概率是:

在第二个位置的概率是：

依次类推，可知该元素将被等概率地分配到任意位置，符合要求。

按该思路实现洗牌算法时有两个问题。首先，新牌堆显然需要的空间；其次，元素从旧数组移入新牌堆后势必会留下空洞，在后续抽牌时要跳过这些空洞位置。

但实际上，新牌堆和旧牌堆元素之和始终为 n，因此整个洗牌过程可以就地完成。我们可以从前向后遍历，对元素 i，前 i-1 个位置构成新牌堆，i 及其后续元素属于旧牌堆。从旧牌堆中随机抽一个元素，与 i 处元素交换，即完成了一次抽牌动作：

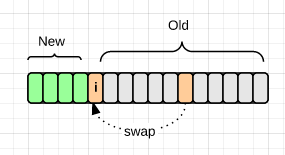
Alt text

这个算法还有个名字，Fisher–Yates shuffle。

代码：

function shuffle(array) {
  var m = array.length, i;

  // While there remain elements to shuffle…
  // 为了方便这里是从后往前遍历的
  while (m) {

    // Pick a remaining element…
    i = Math.floor(Math.random() * m--);

    // And swap it with the current element.
    var t = array[m];
    array[m] = array[i];
    array[i] = t;
  }

}

2. 随机数生成器的转换

听名字有点绕，其实就是给你一个Rand5()，表示随机生成之间的数字，让你实现一个Rand3()。

int Rand3()  
{  
    int x = 5;  
    while(x >= 3) 
        x = Rand5();  
    return x;  
}

逻辑很简单，用Rand5()不停地产生随机数，直到某个数字落在了内。最终只会生成 0/1/2 三个数字，看起来似乎每个数字都是等概率的。下面来证明这个结论：

以输出0为例，看看概率是多少。第一次 Rand5 返回 0 的概率是1/5，如果返回3或4（2/5 的概率），则需要调用第二次，同样的，也是1/5的概率得到 0，2/5 的概率得到3或4导致循环继续执行下去，如此反复。因此输出 0 的概率为：

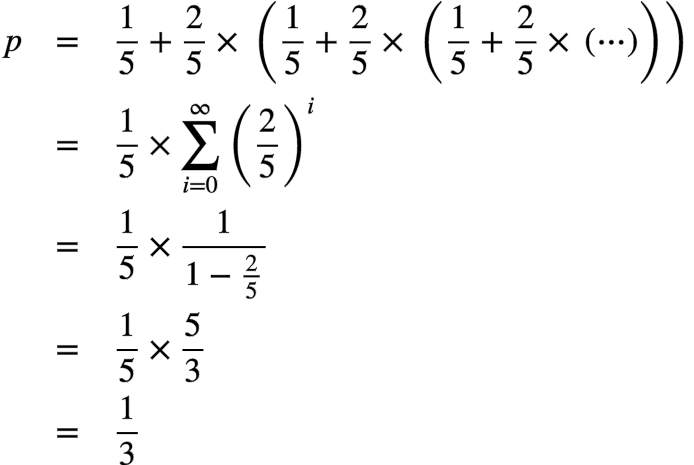
显然这种方法是正确的。

换一下题目，给一个Rand(3)，怎么生成一个Rand(5)呢？由于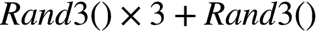可以构造出Rand(9)，对它再应用上述算法即可。

解释下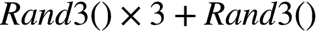为什么可以得到Rand(9)。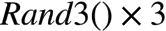得到一个随机数集合0,3,6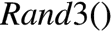，得到0,1,2，二者相加的结果刚好均匀地分布在区间内。推广这个结论可得，可以得到区间内的随机数生成器。

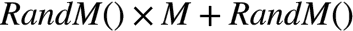
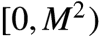
3. 蓄水池抽样

蓄水池抽样是要解决这样一个问题：给定一个很大的集合，集合总数 n 不能确定，只能遍历一遍，要求从中随机选取 k 个元素。

蓄水池算法的原理是：维护一个大小为 k 的蓄水池，用集合的前 k 个元素初始化之；对后续每个元素 i，都以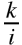的概率替换掉蓄水池中的某个元素。

代码：

Init : a reservoir with the size： k  
for i= k+1 to n  
   M=random(1, i);  
   if( M < k)  
        SWAP the Mth value and ith value  
end for

下面来证明一下该算法的正确性。

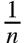
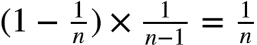
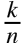
对某个元素，第一次就选中它的概率是，第二次才选中它的概率是，第三次第四次也类似，这跟之前的洗牌场景很像。因此，最终该元素被选中的概率就等于。

当 n == k 时，每个元素出现在蓄水池的概率都是1，即；
当 n == k+1 时，第一次考察发生在元素 k+1 处，根据算法，它被放入蓄水池的概率为；对原蓄水池中的任一元素，该次考察后被换出去的概率等于：

所以，元素依然在蓄水池内的概率为。
当 n == k+2 时，根据2，前 k+1 内的元素在第二次考察（即考察第 k+2 个元素）前在蓄水池内的概率为。

同样的，第 k+2 个元素被放入蓄水池的概率为；

对前 k+1 的元素，在第二次考察后在蓄水池要求 1)之前就在蓄水池；2)这次没有被交换出去：

也符合条件。
推广上述过程即可得证。

几个常见的概率问题

1. 洗牌

2. 随机数生成器的转换

3. 蓄水池抽样

4. 参考