BloomFilter

1. 原理

BloomFilter 是一种基于 bit 数组 + 多重hash 的数据结构，用于判断一个元素是否在一个集合中。

BloomFilter 在内部维护一个长度为 m 的bit数组，并提供 k 个 hash 函数。当一个元素被加入集合时，用这些 hash 函数计算出 k 个数组位置并赋为 1。为了查询一个元素是否在集合中，同样地用 hash 函数计算出该元素在 bit 数组中的 k 个位置，如果全部为 1 就认为在集合中。

当k很大时，设计k个独立的hash function是不现实并且困难的。对于一个输出范围很大的hash function（例如MD5产生的128 bits数），如果不同bit位的相关性很小，则可把此输出分割为k份。或者可将k个不同的初始值（例如0,1,2, … ,k-1）结合元素，feed给一个hash function从而产生k个不同的数。

可以看到，BloomFilter 有两个缺点：

  1. 不支持 remove 元素；
  2. 对一个不在集合中的元素，有可能误判；而且误判率会随着元素的增多而升高。因此不适合要求精确的场合。

BloomFilter 最大的优点是它是基于 bit 数组的，不保存元素本身，因此非常节省空间；同等规模的集合，BloomFilter 占用的空间可能只有 HashSet 的 1/4 或更少。

2. 误判率的计算

m: bit 数组长度
n: 集合元素个数
k: hash 函数个数
p: 误判概率

很显然，误判概率 p 是关于 m/n/k 的函数:

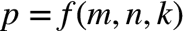
假设一个 hash 函数计算得到的位置等概率地分布在 bit 数组范围内，那么对于一个 bit 位，一次 hash 后它为 0 的概率是：

一个元素被加入集合后，该 bit 依然为 0 的概率是:

n 个元素加入集合后，该 bit 为 0 的概率是：

现在查询一个不在集合中的元素，当它所对应的 k 个位置都为 1 时会发生误判，这个概率 p 是：

由于 当x逼近0时约等于 ，因此有：

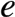
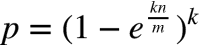
对于该函数，省略推导过程给出结论，如果给定 m 和 n，当 k 取以下值时，误判率 p 的值最小：

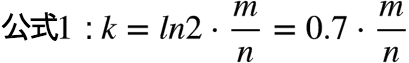
此时误判率 p 等于：

公式1 和 公式2 是实现一个 BloomFilter 需要的理论支撑。

3. 实现

一个 BloomFilter 需要用户提供两个参数：

  1. ，预计集合规模；
  2. ，当元素个数达到 n 时，可以接受的误判率

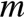
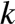
bit 数组长度 和 hash 函数个数 在初始化时由上述两个公式计算而得。

在爬虫项目中用了 BloomFilter 作为 url 的判重器，代码在这里。其中 k 个 hash 函数是通过为 MD5 提供 k 个不同的 salt 构造的。实际使用中当集合规模为 500 万，误判率为万分之一时，所占空间仅为 11.5M。

4. 其他技巧

  1. 两个 BloomFilter 的交集、并集

    filter1 | filter2 == 并集
filter1 & filter2 == 交集

  2. counting BloomFilter

    传统 BloomFilter 只能添加元素，不能对元素计数，也无法删除元素。如果把底层数组的 bit 换成 int，就可以支持计数和删除动作。每次插入元素时，将对应的 k 个 int 加一；查询时，返回 k 个 int 的最小值；删除时，将对应的 k 个 int 减一。

Loading Disqus comments...
目录