贝叶斯
1. 贝叶斯定理
贝叶斯定理是一个关于 条件概率 的公式。所谓”条件概率”(Conditional probability),就是指在事件B发生的情况下,事件A发生的概率,用 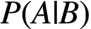
先来看一个问题:
两个一模一样的碗,一号碗有30颗水果糖和10颗巧克力糖,二号碗有水果糖和巧克力糖各20颗。随机选择一个碗并从中摸一颗糖,求抽到1号碗且摸到的是水果糖的概率。
如果把 “抽到1号碗” 称为事件 A,“摸到水果糖” 称为事件 B,问题即求 A/B 两个事件同时发生的概率 ,很明显结果等于
抽到1号碗的概率 * 抽到1号碗后,在1号碗中摸到水果糖的概率:
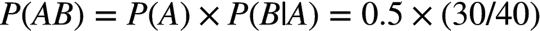
现在换一种问法:
随机选择一个碗,从中摸出一颗糖,发现是水果糖。请问这颗水果糖来自一号碗的概率有多大?
问题变成了求 事件B(从两个碗中摸到水果糖)发生的前提下,事件A(抽到1号碗)的概率,即条件概率 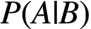
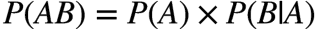
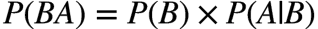
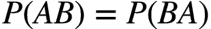
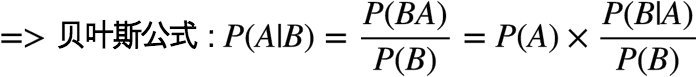
: 抽到1号碗的概率
: 从两个碗中摸到一个水果糖的概率
: 从1号碗中摸到水果糖的概率,为 0.75
假设两个碗是一样的,不考虑摸糖的动作,事件A(即抽到1号碗)的概率 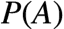
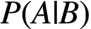
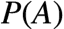
剩下的问题就是如何求 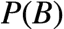
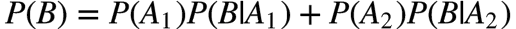
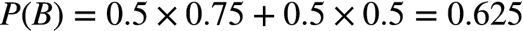
上式亦即所谓的 全概率公式。
最后由贝叶斯公式,有:
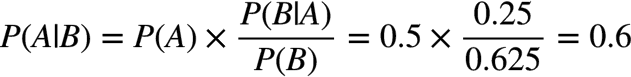
这表明,来自一号碗的概率是0.6。
我们可以看到一个有趣的现象,如果仅选择碗,选中1号的概率是0.5;一旦摸到一颗水果糖,这个概率立刻被增加到0.6,即 摸出水果糖这个事件加强了先验概率。
2. 贝叶斯定理的应用
贝叶斯定理经常被用来计算:当观测到某些事实/特征/数据后, 一个推测成立的概率。
在实际应用中,事件 B 通常是一个已经发生的,可被观测到的数据,而 A 是我们根据事件B提供的数据提出来的一个猜测(假设),后验概率 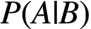
2.1 拼写纠正问题
拼写纠正器需要解决这样一个问题:
当用户输入一个不存在的单词时,他真正是想输入什么单词呢?
我们可以先从词典中找出所有编辑距离为2的单词作为候选单词,但其中哪个单词概率最大呢?在这个问题中,事件 B 是用户已经输入的单词,我们需要找到这样一个单词,使得以下概率最大:
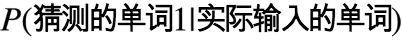
不妨将我们的多个猜测记为 h1 h2 .. ( h 代表 hypothesis),它们都属于一个有限且离散的猜测空间 H (单词总共就那么多而已),将用户实际输入的单词记为 D (Data ,即观测数据),应用贝叶斯公式:
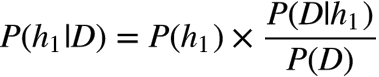
求最佳猜测这种场景中,对所有的猜测而言,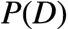
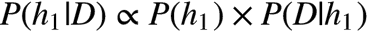
这个结论非常重要,它意味着对于给定观测数据,一个猜测是好是坏,取决于:
猜测自身独立成立的可能性, 即猜测的
先验概率这个猜测下出现观察到的数据的可能性,又称为
似然 Likelihood
判断一个猜测的质量,往往就是这两个因素的拉锯。
回到问题。对于一个猜测的单词,先验概率 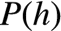
似然 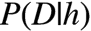
对所有的候选单词都计算一下 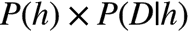
最大似然 & 奥卡姆剃刀
最大似然:如果两个猜测的先验概率一样,那么越符合观测数据的猜测(即 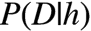
奥卡姆剃刀:如果两个猜测的似然一样,那么优先选更常见更简单(即 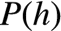
最大似然还有另一个问题:即便一个猜测与数据非常符合,也并不代表这个猜测就是更好的猜测,因为这个猜测本身的可能性也许就非常低。比如 MacKay 在《Information Theory : Inference and Learning Algorithms》里面就举了一个很好的例子:-1 3 7 11 你说是等差数列更有可能呢?还是 -X^3 / 11 + 9/11*X^2 + 23/11 每项把前项作为 X 带入后计算得到的数列?此外曲线拟合也是,平面上 N 个点总是可以用 N-1 阶多项式来完全拟合,当 N 个点近似但不精确共线的时候,用 N-1 阶多项式来拟合能够精确通过每一个点,然而用直线来做拟合/线性回归的时候却会使得某些点不能位于直线上。你说到底哪个好呢?多项式?还是直线?一般地说肯定是越低阶的多项式越靠谱(当然前提是也不能忽视“似然”P(D | h) ,明摆着一个多项式分布您愣是去拿直线拟合也是不靠谱的,这就是为什么要把它们两者乘起来考虑。),原因之一就是低阶多项式更常见,先验概率( P(h) )较大(原因之二则隐藏在 P(D | h) 里面),这就是为什么我们要用样条 来插值,而不是直接搞一个 N-1 阶多项式来通过任意 N 个点的原因。
以上分析当中隐含的哲学是,观测数据总是会有各种各样的误差,比如观测误差(比如你观测的时候一个 MM 经过你一不留神,手一抖就是一个误差出现了),所以如果过分去寻求能够完美解释观测数据的模型,就会落入所谓的数据过配(overfitting) 的境地,一个过配的模型试图连误差(噪音)都去解释(而实际上噪音又是不需要解释的),显然就过犹不及了。所以 P(D | h) 大不代表你的 h (猜测)就是更好的 h。还要看 P(h) 是怎样的。所谓奥卡姆剃刀 精神就是说:如果两个理论具有相似的解释力度,那么优先选择那个更简单的(往往也正是更平凡的,更少繁复的,更常见的)。