背包问题
本文主要讨论01背包/完全背包/多重背包,及在此之上一些常见的变种问题,更复杂的不做讨论。
一. 01背包
1. 基础问法
01背包是所有类型背包问题的基础,它又有各式各样的问法和约束,这些变化同样适用于其他类型的背包问题。
有n个物品,价值v = [v1,v2,v3…],体积c = [c1,c2,c3…],放入总容量为
totalCapacity的背包中,求能获得的最大价值是多少?
背包问题是动态规划的经典问题。动态规划的基础是递归,和分治一样,都是假设子问题已经解决,由子问题的解组合计算得到父问题的解,类似数列中的递推式如f(n) = f(n-1) + f(n-2)。但在递归的过程中会出现重复计算子问题的现象,为了避免重复计算,用一个表格记录子问题的结果供查找,从下往上进行递推。
找递推式(or 状态转移方程)的思路一般是由最终状态往前回溯,考察解答最终问题需要哪些子问题。
背包问题应用动态规划:
- 子问题
根据询问确定子问题,假设f[i][j] = 前i件物品中选取若干件放入空间为j的背包中所能得到的最大价值。 - 递推式:
- 对第i件物品,不选择时,最大价值 = 前i-1件物品获得的最大价值 = f[i-1][j];
- 选择时,最大价值 = 前i-1件物品放入j-c[i]获得的最大价值 + i的价值 = f[i-1][j-c[i]] + v[i];
- 因此,
f[i][j] = max(f[i-1][j],f[i-1][j-c[i]] + v[i]); - 当然,若c[i] > 背包总空间j,物品i只能不选,此时和第一种情况一样。
- 基础子问题的解
f[][0] = 背包空间为0时的最大价值(无法放物品) = 0,f[0][] = 没有物品可放时的最大价值 = 0(物品编号从1开始,0表示不放物品)。
注意,递推过程的是从第二行第二列开始的。
举个例子,当 c=[3,4,5], v=[4,5,6],totalCapacity=10 时,推导过程如下,注意,顺序是从上到下,从左到右一行一行(自底向上)地进行:
| c | v | i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 |
0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |||
| 3 | 4 | 1 | 0 |
0 | 0 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | |
| 4 | 5 | 2 | 0 |
0 | 0 | 4 | 5 | 5 | 5 | 9 | 9 | 9 | 9 | |
| 5 | 6 | 3 | 0 |
0 | 0 | 4 | 5 | 6 | 6 | 9 | 10 | 11 | 11 |
代码:
#!/usr/bin/python
# coding=utf-8
n = 3 # n个物品
c = [None,3,4,5] # capacity -- 注意,物品编号从1开始
v = [None,4,5,6] # value
totalC = 10 # total capacity
def zeroOne():
t = [[None] * (totalC + 1) for i in range(n+1) ] # [n+1][totalCapacity+1]
# 初始化
t[0] = [0] * (totalC + 1) # 第一行为0
for i in range(n+1): # 第一列为0
t[i][0] = 0
for i in range(1,n+1): # 从第二行第二列开始扫描. i: 当前考察的物品, j: 总空间
for j in range(1,totalC+1):
if c[i] > j: # 无法放入第i个物品 -- 必定不选
t[i][j] = t[i-1][j]
else: # 可以放入第i个物品 -- 可能选,可能不选
t[i][j] = max(t[i-1][j], t[i-1][j-c[i]] + v[i])
return t
if __name__ == "__main__":
print zeroOne()[n][totalC]时间和空间复杂度为O(n*totalCapacity)。
2 求最大价值时的物品选择方案
求最大价值下的物品选择方案有两种办法:
1..从后面往前,根据递推式依次看第i..1个物品有没有被选择:
t = zeroOne()
# print path 方法1
i = n
j = totalC
while i > 0 and j > 0:
if t[i][j] != t[i-1][j]: # 选了第i个物品
print "第%s个物品,空间:%s,价值:%s" % (i,c[i],v[i])
j -= c[i]
# 考察前一个物品
i -= 12..在求最大价值的同时用一个n*totalCapacity大小的二维数组path记录每个物品是否选择:
def zeroOneWithPath():
t = [[None] * (totalC + 1) for i in range(n+1) ] # [n+1][totalCapacity+1]
path = [[0] * (totalC + 1) for i in range(n+1) ] # path, 0没选,1选了
# 初始化
t[0] = [0] * (totalC + 1) # 第一行为0
for i in range(n+1): # 第一列为0
t[i][0] = 0
for i in range(1,n+1): # 从第二行第二列开始扫描. i: 当前考察的物品, j: 总空间
for j in range(1,totalC+1):
if c[i] > j: # 无法放入第i个物品 -- 必定不选
t[i][j] = t[i-1][j]
else: # 可以放入第i个物品 -- 可能不选,可能选
t[i][j] = max(t[i-1][j], t[i-1][j-c[i]] + v[i])
# 如果选择了第i个物品,记录path
if t[i][j] == t[i-1][j-c[i]] + v[i]: # <----- 只有这一个改动
path[i][j] = 1
return t,path求物品选择方案的方法和前一种办法是一模一样的,只不过现在是根据path中的标记位,而不是最大价值与递推式来判断是否选择了该物品:
# print path 方法2
t,path = zeroOneWithPath()
i = n
j = totalC
while i > 0 and j > 0:
if path[i][j] == 1: # 选了第i个物品 # <----- 只有这一个改动
print "第%s个物品,空间:%s,价值:%s" % (i,c[i],v[i])
j -= c[i]
i -= 1实际上,两种方法的思路是一样的,不过方法2消耗的空间更多,但下面要讲的O(n)空间复杂度的算法只能使用方法2。
3 空间优化
接下来讨论怎样将算法的空间复杂度降低到O(totalCapacity)。实际上,这里用到的思路就是所谓的 滚动数组:
很多情况下,一个问题的解仅由其前面有限个子问题决定,除了这些子问题,之前记录的规模更小的子问题的解都可以舍去,所以,可以用更少的空间只保存这些子问题的解并循环利用,从而避免保存所有子问题的解。
举个例子,斐波那契数列问题中,f(n)=f(n-1)+f(n-2),当n为5时,f(5)仅与f(4)和f(3)有关,f(0)..f(2)都没有用了。因此,我们可以只用两个变量不停地维护f(n-1)和f(n-2),而不是将f(0)..f(n-1)的结果都保存起来。
回到01背包问题,求某个格子时,其值是由上一行的某两个格子(正上方的格子和左侧某一个格子)决定的,与更早的行没有关系,这些行的空间都被浪费了:
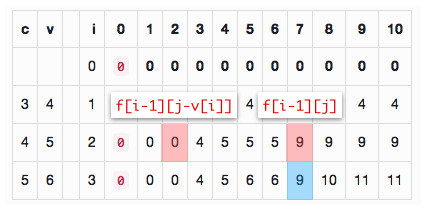
所以,我们可以只用一行的空间保存前一行的值并循环利用,而不需要一个表格。但此时 递推顺序不能是从左到右了,而是应该反过来,因为如果是正序,在递推的时候用的就是第i行的新值,而非前一行的数据了。实际上,用表格时也可以从右到左递推。
代码:
def zeroOne2():
t = [0] * (totalC + 1)
for i in range(1,n+1): # for i in 1..n, i是物品编号
for j in reversed(range(c[i],totalC+1)): # for j in totalC..c[i], j是背包总空间 //j<物品体积c[i]时,i必定不选,c[i][j]=c[i-1][j],不用考察
t[j] = max(t[j],t[j-c[i]] + v[i])
return t
if __name__ == "__main__":
print zeroOne2()[totalC]时间复杂度仍为O(n*totalCapacity),空间复杂度降低到了O(totalCapacity)。此时如果想要求最优价值的物品选择方案,只能用额外的path表格记录。
此类优化方式大部分的背包问题都可应用,后续不再赘述。
4 要求刚好装满
背包问题常见的一个限制是需要背包刚好装满,在该约束下需要注意两点:
- 在使用递推式推导的过程中必须考虑 子问题是否有解 ;
- 基础子问题的含义/解
当求最大价值时,规定当无解时用NULL表示,其他值表示刚好能装满的最大价值:
- 第一列 f[][0] = 背包空间为0,认为永远是满的,且无法放物品 = 0
- 第一行(除第一个) f[0][1..totalCapacity] = 没有物品可放,此时除了空间为0的背包,其他背包永远不可能放满 = NULL
- 其他变种问题类似。
以上两点适用于所有需要装满背包的场景。
求最大价值的推导过程如下:
| c | v | i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 |
Null | Null | Null | Null | Null | Null | Null | Null | Null | Null | |||
| 3 | 4 | 1 | 0 |
null | null | 4 | null | null | null | null | null | null | null | |
| 4 | 5 | 2 | 0 |
null | null | 4 | 5 | null | null | 9 | null | null | null | |
| 5 | 6 | 3 | 0 |
null | null | 4 | 5 | 6 | null | 9 | 10 | 11 | null |
代码:
def zeroOneFullPack():
t = [[None] * (totalC + 1) for i in range(n+1) ] # [n+1][totalCapacity+1]
# 初始化
t[0] = [None] * (totalC + 1) # t[0][1..totalCapacity] = None
for i in range(n+1): # t[][0] = 0
t[i][0] = 0
for i in range(1,n+1):
for j in range(1,totalC+1):
if c[i] > j: # 无法放入第i个物品 -- 必定不选
t[i][j] = t[i-1][j]
else: # 可以放入第i个物品
a = t[i-1][j-c[i]] # a: 前i-1个物品放入j-c[i]空间
b = t[i-1][j] # b: 前i-1个物品放入j空间
if a != None and b != None: # a和b都有解,则用递推式
t[i][j] = max(b,a + v[i])
elif a == None and b == None: # a和b都无解,则无解
t[i][j] = None
elif a == None: # a无解而b有解,此时一定不能选择物品i,选择则无解
t[i][j] = b
elif b == None: # a有解而b无解,此时只能选择i,不选则无解
t[i][j] = a + v[i]
return t
if __name__ == "__main__":
print zeroOneFullPack()[n][totalC]5 只考虑物品空间,忽略价值
有时题目只关心物品的体积,而不涉及物品的价值,下面提到的几类问题都是如此。
5.1 求能获取的最大体积
比较常见,简化的01背包问题,每个物品的价值即为其体积,代码略。
例子:
- 给一个整数的集合,要把它分成两个集合,要两个集合的数的和最接近
5.2 求刚好装满背包的方案数
类似的:
- 子问题
f[i][j]为前i件物品放入j空间,刚好装满的方案数,无解时为0 - 递推式
f[i][j] = f[i-1][j] (不选i) + f[i-1][j-c[i]] (选i)
如果不选i,”前i件物品装满j空间的方案数” 等于 “前i-1件物品装满j空间的方案数” ;选i,则等于”前i-1件物品装满j-c[i]空间的方案数”。二者相加即为f[i][j]。- c[i] > j时一定不能选i,f[i][j] = f[i-1][j]
- 基础子问题的解
和 求装满条件下最大价值 的场景一样,
- 第一列 f[][0] = 背包空间为0,认为永远是满的,只有一种装满的方案(不放物品) = 1
- 第一行(除第一个) f[0][1..totalCapacity] = 没有物品可放,此时除了空间为0的背包,其他背包永远不可能放满 = 0
def waysToFillPack():
t = [[None] * (totalC + 1) for i in range(n+1) ] # [n+1][totalCapacity+1]
# 初始化
t[0] = [None] * (totalC + 1) # t[0][1..totalCapacity] = None
for i in range(n+1): # t[][0] = 1
t[i][0] = 1
for i in range(1,n+1):
for j in range(1,totalC+1):
if c[i] > j: # 无法放入第i个物品 -- 必定不选
t[i][j] = t[i-1][j]
else:
a = t[i-1][j-c[i]] # a: 前i-1个物品放入j-c[i]空间
b = t[i-1][j] # b: 前i-1个物品放入j空间
if a != None and b != None: # a和b都有解,则用递推式 <---- 仅仅递推式不同而已
t[i][j] = a + b
elif a == None and b == None: # a和b都无解,则无解
t[i][j] = None
elif a == None: # a无解而b有解,此时一定不能选择物品i
t[i][j] = b
elif b == None: # a有解而b无解,此时只能选择i
t[i][j] = a
return t例子:
- 有不同面额的若干钱币,每种面额只有一个,求表示给定面值的方案数
5.3 求刚好装满背包的最少/多选择物品数
以最少为例:
- 子问题
f[i][j]为前i件物品放入j空间,刚好装满的最少物品数,用None表示无解 - 递推式
f[i][j] = min{ f[i-1][j] (不选i), f[i-1][j-c[i]] + 1 (选i) }- c[i] > j时一定不能选i,f[i][j] = f[i-1][j]
- 基础子问题的解
- 第一列 f[][0] = 背包空间为0,认为永远是满的,选择物品数为0 = 0
- 第一行(除第一个) f[0][1..totalCapacity] = 没有物品可放,此时除了空间为0的背包,其他背包不存在装满的方案 = None
# 装满时的最少物品数
def leastObjFillPack():
t = [[None] * (totalC + 1) for i in range(n+1) ] # [n+1][totalCapacity+1]
# 初始化
t[0] = [None] * (totalC + 1) # t[0][1..totalCapacity] = None
for i in range(n+1): # t[][0] = 0
t[i][0] = 0
for i in range(1,n+1):
for j in range(1,totalC+1):
if c[i] > j: # 无法放入第i个物品 -- 必定不选
t[i][j] = t[i-1][j]
else:
a = t[i-1][j-c[i]] # a: 前i-1个物品放入j-c[i]空间
b = t[i-1][j] # b: 前i-1个物品放入j空间
if a != None and b != None: # a和b都有解,则用递推式
t[i][j] = min(b,a+1)
elif a == None and b == None: # a和b都无解,则无解
t[i][j] = None
elif a == None: # a无解而b有解,此时一定不能选择物品i
t[i][j] = b
elif b == None: # a有解而b无解,此时只能选择i
t[i][j] = a + 1
return t例子:
- 有不同面额的若干硬币,每种面额只有一个,求最少需要多少硬币表示给定面值
除了上述几种情况,背包问题还有很多其他变种,不过基本思路和递推过程都是一样的,其核心都在于 1)根据询问的不同找到正确的递推式(min|max|sum...);2)确定基础子问题的解。
二. 完全背包
1. 基本解法
完全背包指每种物品有无数件,它和01背包的区别只有递推式的一个地方:
- 01 : f[i][j] = max(f[i-1][j],
f[i-1][j-c[i]]+ v[i]) - 完全:f[i][j] = max(f[i-1][j],
f[i][j-c[i]]+ v[i])
解释:
考虑第i种物品,若不选,则f[i][j] = f[i-1][j];若选择,意味着至少有一件i物品,考虑这一件物品,剩余j-c[i]空间用来放 0..i种 物品(i依然能放),这部分空间的最大价值为f[i][j-c[i]]。综合即可得到上述公式。
直观的,在递推时,01背包依赖的是上一行的某两个格子(正上方和左侧),完全背包则依赖上一行正上方的格子 + 同一行左侧的某个格子。
2. 空间优化
与01背包类似,但是这里遍历顺序 不要逆序 了,即此时需要从左向右递推。因为01背包递推时f[i-1][j-c[i]]是上一行的值,而完全背包f[i][j-c[i]]则刚好是本行的新值。
三. 多重背包
指的是第i个物品有n[i]件,此时直观上可以将每个物品拆成n[i]个单个物品,转化为01背包问题。但当n[i]比较大时物品件数将急剧增加,为了避免这种情况可以使用 二进制拆分法,降低拆分后的物品数。
1. 二进制拆分
原理:
一个正整数n可以被分解成1,2,4,…,2^(k-1),n-(2^k+1)(即n-前面数的和), k是满足n>2^k+1的最大整数,且1~n之内的所有整数均可以唯一表示成这些数中某几个数的和的形式。
代码更容易理解些:
var result = [];
var n = ..;
// 1,2,4,8...直到>n (不包括最后一个数字)
for(i=1;i<=n;i*=2){
result.push(i);
n-=i;
}
// n剩下的部分
if(n>0)
result.push(n);比如13可以拆分成1/2/4/6,1~13均可由这些数凑成。将件数为13,价值为v的物品拆分成1*v,2*v,4*v,6*v这4件物品后,该物品的任意选择(1件/2件..13件)均可由它们表达,如选择10件该物品 = 选择物品4*v + 选择物品6*v。和简单拆分相比,该拆分方式不但达到了同样的效果,拆分后的个数也由n下降到log2(n),即n的二进制表示的位数。