并查集

概述

树形数据结构，通常用来解决连通集合相关的问题。

一个容量为n的集合，对应的并查集是一个等长数组，a[i] 保存着第i个元素的父节点，这样递归地组成若干棵树，每个树是一个连通集合，树根的父节点指向自己。

操作

并查集最基本的两个操作：

1. 查询元素所在集合 findSet(i)

   从元素 i 向上回溯找树根即可。一个集合由其根元素标识。

2. 合并集合 union(i,j)：合并元素 i，j 所在集合

   分别找到 i，j 所在集合的根，将其中一个挂在另一个下即可。
   

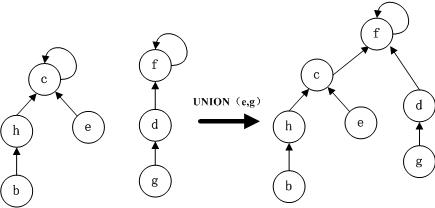
初始化：每个元素独立成为一个集合。

优化

1. findSet 路径压缩
极端情况下一棵集合树退化成一个链表，此时查找根节点耗时O(n)。findSet中可以做这样一个优化：在找到根后，将路上碰到的节点都直接挂在根下，树的高度被压缩成了2，之后的查询都是O(1)的。这是一个扁平化树的过程：

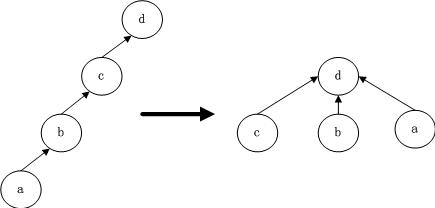
2. union 按集合大小合并
合并的时候将元素少的集合合并到元素多的集合中，这样合并之后树的高度会相对较小。

这两个动作都可以认为是O(1)的。

实现

#! /usr/bin/python
# coding=utf-8

raw = [8,3,5,6,8,9,1,3]
set = range(len(raw))   # 并查集 [0,1,2...]
size = [1] * len(raw)   # 每个集合的大小

def findSet(i):
    if set[i] == i:
        return i

    set[i] = findSet(set[i])
    return set[i]

def union(i,j):
    root1 = findSet(i)
    size1 = size[root1]

    root2 = findSet(j)
    size2 = size[root2]

    if size1 > size2:       # 把2挂在1下
        set[root2] = root1
        size[root1] += size2
        size[root2] = 0
    else:                   # 把1挂在2下
        set[root1] = root2
        size[root2] += size1
        size[root1] = 0

# 测试
def test():
    print size[3],size[5]   # 1,1
    union(3,2)
    union(1,2)              
    union(5,6)
    print findSet(3) == findSet(1), findSet(5) == findSet(6) # True True
    print size[findSet(1)],size[findSet(5)] # 3,2

test()