线段树
结构
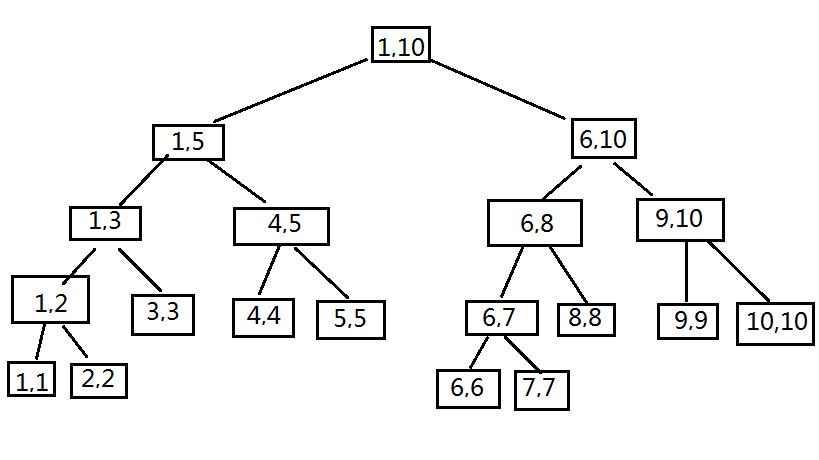
特点:
- 完全二叉树
- 每个节点代表一个区间,孩子节点分别代表两个子区间
- 节点保存着 该区间内问题的解,以及求解需要的其他数据
用一个数组保存,和 heap 结构类似。
分治,要求能够从若干子区间的解推导出父区间的解,且对父区间的更新可以传导给子区间
适用于区间查询 / 区间维护等问题
操作
线段树支持以下操作:
- 构造
- 更新
- 单点更新
- 区间更新
- 区间查询
以区间和问题为例:
构造
O(N)
tree = None
#### Utils
def eval(i):
"""
由孩子节点计算某节点的 sum
"""
tree[i]['sum'] = tree[lc(i)]['sum'] + tree[rc(i)]['sum']
def lc(i):
"""
左孩子
"""
return 2*(i+1) - 1
def rc(i):
"""
右孩子
"""
return 2*(i+1)
def mid(i):
"""
计算节点所代表区间的中间位置
"""
return tree[i]['start'] + (tree[i]['end']-tree[i]['start'])/2
####
def init(array):
global tree
# 计算线段树节点个数,完全二叉树的节点数 = 2^(height+1) - 1
length = len(array) # range length
height = math.ceil(math.log(length,2))
maxSize = int(math.pow(2,height + 1) - 1)
_init(array,0,0,length - 1) # 默认区间为数组下标区间
def _init(array,i,s,e):
"""
构造一棵线段树,节点格式:{start:1,end:2,sum:8}
array -- 原始数组
i -- 根节点
s -- 根节点代表的区间开始处
e -- 根节点代表的区间结束处
"""
tree[i] = {'start':s,'end':e,'sum':None}
## 如果是原子区间,即叶子节点
if s == e:
tree[i]['sum'] = array[s]
return
_init(array, lc(i), s, mid(i))
_init(array, rc(i), mid(i) + 1, e)
eval(i)单点更新
O(log2N)
def update(i,value):
_update(0,i,value)
def _update(root,i,value):
# 找到了这个点,更新其sum并返回
if tree[root]['start'] == i and tree[root]['end'] == i:
tree[root]['sum'] = value
return
if i<= mid(root):
_update(lc(root),i,value)
else:
_update(rc(root),i,value)
eval(root)区间更新
O(log2N)
基本思路是将要修改的区间顺着根一层一层往下查找,直到找到一批子区间刚好组成目标区间,再将更新动作应用在这些区间内。比如文章开始的线段树中,如果要更新[1,7],则可以在树中找到节点[1,5], [6,7]刚好凑成[1,7],更新这两个区间,重新计算二者祖先节点值即可。
问题是[1,5]并不是叶子节点,如果将以它为根的整个子树全部更新,那么一次更新的动作涉及到的节点就很多了。因此引入延迟更新的思路:
当更新[1,5]时,只更新该节点,并给它加上一个更新动作的标记,子节点不更新。
查询或修改时,如果碰到了节点[1,5],并决定进入其子节点考察,为了不访问到错误的值,需要看[1,5]的更新标记,如果有,则将更新动作应用到子节点,并清除自身的标记。子节点的更新则继续 lazy 的思路。
def rangeUpdate(start,end,value):
_rangeUpdate(0,start,end,value)
def _rangeUpdate(root,start,end,value):
"""
线段树的区间update,必须满足父区间的update可以传递到左右子区间.
-- 即update(a,b)的效果 等价于 update(a,i) & update(i+1,b).
lazy update后,其子树的data是过时的, 因此 rangeUpdate 和 query 时,在进入孩子节点考察前,必须先将父节点的 update 动作推送给它的左右孩子。
"""
# 到了某个最大组成子区间,lazy更新并返回
if tree[root]['start'] == start and tree[root]['end'] == end:
tree[root]['sum'] = (end - start + 1) * value
tree[root]['update'] = value # 标记
return
# 推送更新动作到子区间
_pushDownUpdate(root)
# 更新子区间
if end <= mid(root):
_rangeUpdate(lc(root),start,end,value)
elif start > mid(root):
_rangeUpdate(rc(root),start,end,value)
else:
_rangeUpdate(lc(root),start,mid(root),value)
_rangeUpdate(rc(root),mid(root) + 1,end,value)
# 子区间更新完毕,重新计算当前节点的值
eval(root)
def _pushDownUpdate(parent):
"""
将update动作传递给孩子
"""
p = tree[parent] # parent
if 'update' in p:
u = p['update']
l = tree[lc(parent)] # left child
r = tree[rc(parent)] # right child
# 给左右子区间记录update动作
l['update'] = r['update'] = u
# 更新左右子区间
l['sum'] = (l['end'] - l['start'] + 1) * u
r['sum'] = (r['end'] - r['start'] + 1) * u
# 清除父区间的update动作
del p['update'] 区间查询
O(log2N)
找最大组成子区间,merge结果
def query(start,end):
return _query(0,start,end)
def _query(root,start,end):
"""
对root的子区间进行查询, [start,end]必须是root所代表的子区间
"""
# 查询的区间就是root的区间时,直接返回root保存的data
if tree[root]['start'] == start and tree[root]['end'] == end:
return tree[root]['sum']
_pushDownUpdate(root)
# [start,end]:
# 1. 如果在左子区间内,进入左子树
if end <= mid(root):
return _query(lc(root),start,end)
# 2. 如果在右子区间内,进入右子树
if start > mid(root):
return _query(rc(root),start,end)
# 3. 跨越了左右子区间,则将[start,end]拆分为[start,mid] & [mid+1,end],
# 分别进入左右子树查询,并merge这两个区间上的查询结果
return _query(lc(root),start,mid(root)) + _query(rc(root),mid(root) + 1,end)