LCA 和 RMQ

这篇文章主要谈谈 LCA (lowest common ancestor) ，即最近公共祖先问题的常见解法。

1. 转换成链表交点问题

如果节点 i/j 内维护父节点的指针，则可以很容易地找到 i/j 到根节点的路径，问题变成了求两条链表在何处相交：

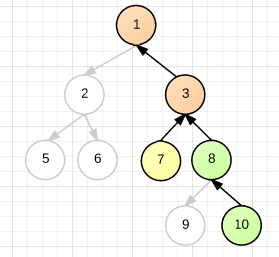
上图中，7 和 10 的 LCA 即为 7-3-1 与 10-8-3-1 两条链表的交点 3。

链表交点可以这样求：

遍历得到两条链表长度之差 m，再用两个指针分别指向两个 head，让长链表的那个指针先走 m 步，然后两个指针同时移动，直到指向同一个节点，该节点即为交点，如下图所示：

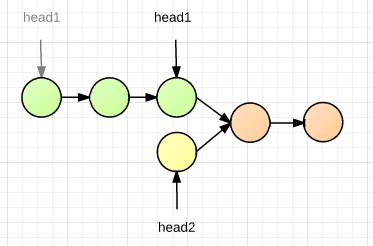
2. 利用 DFS 转换成 RMQ (在线)

该算法的基本原理是，如果把一棵树 DFS 走过的路径 Path 记录下来（包括回溯时经过的节点），对于两个节点 i 和 j ，找到他们第一次出现在 Path 的位置，这之间的序列就表示 DFS 过程中从节点 i 出发访问到 j 的轨迹，其中，高度最低的节点即为二者的 LCA。

以下图为例

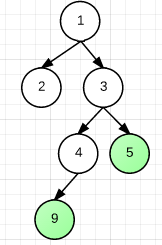
DFS路径如下：

1  2  1  3  4  9  4  *3*  5
               ￣         ￣

9 到 5 的轨迹为 9-4-3-5，其中 3 最矮，它就是 9 和 5 的 LCA。

实现上述逻辑需要两个数据结构：

1. DFS 路径 path，每个元素还得额外保存节点高度；

   对一棵二叉树而言，每个节点在 DFS 的过程中最多出现两次，因此 path 的长度最多为 2n。

2. 一个 map firstOccur，保存每个节点在path中第一次出现的位置。

于是问题转换为 RMQ。对 RMQ，线段树是一种可行的解法，它需要 的建树时间， 的查询时间。

这里介绍另一种基于动态规划，名为 Sparse Table 的算法。

Sparse Table 算法

Sparse Table 算法用一个表格记录某些特定区间的最小值，任意区间都可以分解为其中的两个（可能重叠的）子区间。它需要 时间预处理，每次查询耗时 ；空间复杂度为 。

预处理

首先需要一个矩阵 m，m[i][j]表示从索引 i 开始连续 个数，即区间 中的最小值。例如数列 a：

3 2 4 5 6 8 1 2 9 7

m[0][0] 表示从 0 开始，长度为 的最大值，即3；因此 m[i][0] 就等于a[i]，这就是 DP 的初始状态，也即 DP 表格的第一列。

接下来就是递推式了。由于m[i][j]代表的区间长度肯定是偶数，因此可以将其平均分成两段：

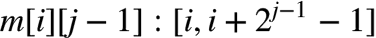
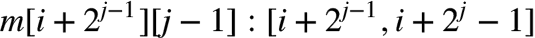
递推式也就出来了：

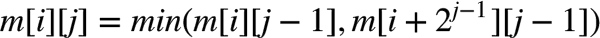
这个 DP 是从左向右一列一列进行的。

查询

给定一个任意区间[i,j]，我们找到满足 (区间内元素个数) 的最大的 k，则有:

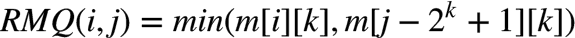
举个例子，对于区间 [3,9]，取 k = 2 ，m[3][2] 和 m[6][2] 将这7个元素划分为两个 重叠 的部分，靠左4个，靠右4个，最小值即为它们中最小的那个。

3. Tarjan 算法 (离线)