KMP
1. KMP原理
暴力求解时使用两个指针i和j,匹配失败时,i回溯至该次匹配起始点+1的位置,j回溯至0,然后继续同时移动匹配,复杂度为O(m*n)。KMP的精髓在于,当匹配失败时能够利用已经匹配成功的j个字符的性质回溯j指针,不需要回溯i,从而将遍历txt的时间缩短为O(m)。
举例说明,假设txt=”abababaabab”,pattern=”ababacb”,初始i=j=0,开始同时往右移动进行匹配,第一次匹配失败时的情况如下所示:
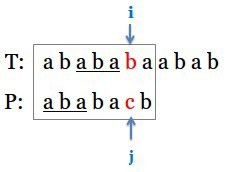
方框表示的是当前Pattern正和Txt中哪部分子串进行比对。
此时,注意到 从i往前回溯3个字符 和 pattern开始的3个字符 是一样的,如图中下划线所示,都是“aba”,我们可以利用这个特点,不回溯i,直接回退j到“aba”的后面,i、j再次同时右移进行比较,如下图所示:
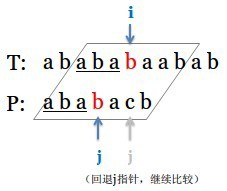
回溯j时,我们充分利用了已经匹配成功的部分子串的“对称性”,即从匹配失败的i处开始往前,总有一小部分字符是和Pattern的前几个字符相同的,在刚刚的例子里是“aba”(姑且称之为“对称子串”)。因此,在下次匹配时可以将j回退到该对称子串的右侧,直接跳过这些字符,再同i匹配;如果没有对称子串,j只能回溯到0,这种情况的处理下面会提到。不管是哪种情况,都不需要回溯i指针。
ok,此时i和j指向的元素恰好相同,于是继续同时右移,下一次匹配失败发生在两步之后:
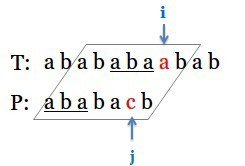
同样的,找到失败时的 已匹配子串“ababa”的对称子串“aba”(如图中下划线所示),将j回退到该子串的右侧继续和i同时右移比对,于是便成了:
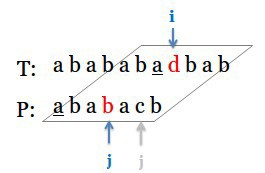
i和j继续比对,这次立马就失败了,于是继续回溯j到对称子串“a”的右侧:
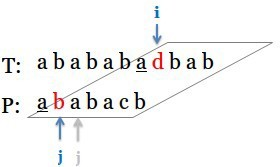
继续比对,但这次还是失败,j只能回溯到0。当j==0时,固定j,i向右移动直到txt[i] == pattern[0]:
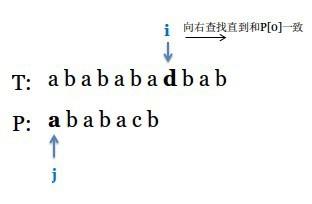
重复以上的过程,当j指向pattern最后一个元素且i、j对应的字符相等时,匹配成功。
问题来了,当回溯j时如何知道要回溯到哪个位置?根据前文的描述,当匹配失败时,j需要回溯到前j-1个字符的“对称子串”的右侧(没有则回溯到0),而对称子串仅与pattern本身的性质(对称性)有关,因此,我们完全可以预处理pattern,对每个位置j,计算出当在j处匹配失败时 j需要回退的位置,存放这些信息的数组我们称之为next数组。
总结一下利用next数组进行匹配的过程:
- i=j=0;
- j和i同时往右走进行比对,相等时若j指向pattern最末则匹配成功,失败时j根据next[j]回退并继续比对;
- 每次回退后判断j是否==0,j==0时固定j,i向后遍历直到txt[i] == pattern[0],此时跳转到2。
将上述逻辑“直译”成代码则如下所示:
public int search(String txt) {
int i = 0, j = 0;
int txtLen = txt.length();
int patternLen = pattern.length();
while (i < txtLen) {
// i/j同时右移匹配
for (; txt.charAt(i) == pattern.charAt(j); i++, j++) {
//j指向pattern最末时,匹配成功
if (j == patternLen - 1)
return i - j;
}
// 匹配失败,j回溯
j = next[j];
// j回溯至0时,i向后遍历直到txt[i]和pattern[0]相等
if (j == 0) {
while (i < txtLen && txt.charAt(i) != pattern.charAt(0))
i++;
}
}
return -1;
}代码可以更精简,但目前这样更方便我自己记忆和理解整个逻辑。
2. Next数组
现在考虑怎么求next数组,我们知道,next[j]有两重含义:
Pattern[0 ... j-1]的(最大)对称子串长度 =next[j]:即
Pattern[0 ... j-1]的前next[j]个字符和后next[j]个字符是相同的;在j处匹配失败时,j指针需要回退的位置:
即
Pattern[0 ... j-1]的对称子串的右侧;不存在对称子串时next[j]=0,表示j必须回退到第一个元素。
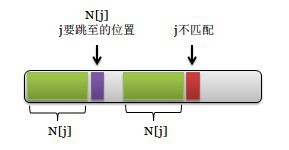
最简单的求法是用两个指针在0 … j-1段一个往后一个往前探测,但每求一个位置的next[j]都要这个过程,显然重复了很多计算工作。实际上,next[j+1]可以由已经求的的next[0] … next[j]计算得到。先看 next[j] 和 next[j+1] 的关系,next[j]的含义是 0…j-1 的最大对称子串长度,此时只需查看 pattern[ next[j] ] 和 pattern[j] (如下图黑色箭头所指),如果二者相等,那么next[j+1] = next[j] + 1,如下图所示:
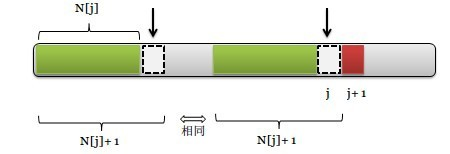
如果运气没那么好,这两个元素不等,该怎么办?我们可以继续考察0…j-1的最大对称子串的对称性,即上图中的绿色区域的对称性,如下所示:
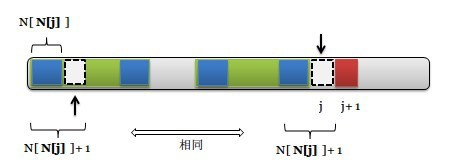
此时我们要拿 next[ next[j] ] 指向的元素(上图第一个箭头)和pattern[j](上图第二个箭头)比较,如果相等则next[j+1] = next[ next[j] ] + 1;如果不等则循环这个过程。可以想象成不停地缩小查找的对称区域,一开始是查看j左侧所有元素的对称子串,接下来是该对称子串(绿色部分)的对称子串(蓝色部分),不满足条件就接着查看对称子串的对称子串的对称子串。。。
当遇到0时循环结束,说明查找完所有可能的对称子串都不满足要求,此时我们只能查看pattern[0]和pattern[j],如果相等,next[j+1]=1,说明0 ... j的最大对称子串长度为1;否则=0,说明0 ... j内不具有对称性。
将上面这个过程翻译过来,代码如下:
private int[] next;
private String pattern;
public KMP(String pattern) {
this.pattern = pattern;
next = new int[pattern.length()];
// 初始化next[0]和next[1],均为0
next[0] = 0;
if (pattern.length() <= 1)
return;
next[1] = 0;
loop: for (int j = 2; j < pattern.length(); j++) {
int pre = j - 1; // j前一个元素,在寻找过程中要和它做比较
int k = next[pre];
while (k != 0) {
// 查找成功,进行下次循环,求next[j+1]
if (pattern.charAt(pre) == pattern.charAt(k)) {
next[j] = k + 1;
continue loop;
}
// 否则继续查找内部对称子串
k = next[k];
}
// k == 0,说明没有满足要求的对称子串,只能查看pattern[0] 和 pattern[pre]是否相等
next[j] = pattern.charAt(pre) == pattern.charAt(0) ? 1 : 0;
}
}同样的,代码也不是最精简的,但是和之前描述的逻辑是一致的,更容易看懂和理解。
3. 复杂度
- 时间复杂度:
O(m+n)//遍历txt+生成next数组 - 空间复杂度:
O(n)//next数组 - 时间复杂度的分析要用到“摊还分析”,看了很久还没太理解,暂且按下不表。
4. 测试
public static void main(String[] args) {
String pattern = "PARTICIPATEINPARACHUTE";
KMP rk = new KMP(pattern);
String txt = "fdjkajjjfppPPPPPPPPPARTICIPATEINPARACHUTE";
System.out.println(txt);
int index = rk.search(txt);
if (index >= 0) {
for (int i = 0; i < index; i++) {
System.out.print(" ");
}
System.out.print(pattern);
}
}输出
fdjkajjjfppPPPPPPPPPARTICIPATEINPARACHUTE
PARTICIPATEINPARACHUTEnext数组为: