Hash & Rabin-Karp字符串查找算法

1. Hash函数

将若干元素均匀的映射到一个空间（大小为M）的各个位置，常用于快速查找。

正整数

最常用的函数：“%”, `hash = key % M`

M一般是素数，否则可能无法利用key中包含的所有信息。如key是十进制数而M是10的k次方，那么只能利用key的后K位，不均匀，增加碰撞概率。

字符串

%也适用于字符串，只需要将字符串看成一个若干位R进制的整数，不同的是R并不一定非得大于字符集的个数，可以适当进行调整，常常选取质数。

代码：

public int hash(String s,int M){
    int hash = 0;
    int R = 101;    //进制
    /*
        Horner's rule:
        hash(abc)=a*R^2 + b*R^1 + c*R^0 = ((a*R + b) * R) + c

    */
    for(int i=0;i<s.length();i++){
        hash = R * hash + s.charAt(i);
    }
    return hash % M;
}

这种计算方式当charAt方法返回的值过大或R太大时可能造成溢出，可以将第10行换成：

hash = (R * hash + s.charAt(i)) % M;

这利用了%运算的基本性质，对于两个正整数a、b，有：

(a+b)%n = (a%n + b%n) %n;
(a-b)%n = (a%n - b%n + n) %n;
(a*b)%n = (a%n * b%n) %n;

注意，在减法中，由于a%n 可能小于b%n，需要在结果上加上n。对于以上规则，a和b不需要同时%n，可以随意选取一方%n性质也成立。

2. Java的hashCode()

将每个对象映射到Integer空间（因为返回值是int），由hashCode的调用方决定是否需要进一步映射到一个更小的空间，比如在HashSet这种场景。

JDK为String类的hashCode提供了默认的实现：

/**
 * Returns a hash code for this string. The hash code for a
 * <code>String</code> object is computed as
 * <blockquote><pre>
 * s[0]*31^(n-1) + s[1]*31^(n-2) + ... + s[n-1]
 * </pre></blockquote>
 * using <code>int</code> arithmetic, where <code>s[i]</code> is the
 * <i>i</i>th character of the string, <code>n</code> is the length of
 * the string, and <code>^</code> indicates exponentiation.
 * (The hash value of the empty string is zero.)
 *
 * @return  a hash code value for this object.
 */
public int hashCode() {
int h = hash;
if (h == 0) {
    int off = offset;
    char val[] = value;
    int len = count;

        for (int i = 0; i < len; i++) {
            h = 31*h + val[off++];
        }
        hash = h;
    }
    return h;
}

使用的算法和上面描述的一致，R选择的是31。

具体的 HashMap 负责将 hashCode 映射到更小的空间，常用的方式是屏蔽符号位并取模：

int hash(Object x){
    return (x.hashCode() & 0x7fffffff) % M;
}

3. 碰撞

碰撞的常规解决办法有拉链法（链表数组）、开放定址法，这里不多做介绍。

不需要存储元素，只需要比较、判重时，可以采用 ：

  1. 元素较少且比较随机时，使用一个巨大的映射空间（比如M=一个巨大的素数、直接MD5等等，空间不需保存不占内存），碰撞概率为1/M；

    碰撞的概率很低很低，相信概率的力量。

  2. 元素很多时，进行k次hash，降低碰撞率

    BloomFilter就是这么干的，加入的元素个数在某个阈值内时能保证错误率在可接受范围内，再多的话碰撞的概率就不行了。

4. Rabin-Karp子字符串查找算法

对于查找，第一反应就是hash，但是假设计算子串的hash为O(k)，遍历一遍原字符串计算每个子串的hash与pattern字符串的hash作比较，复杂度为O(n*k)，这和暴力比较是一样的。

Rabin-Karp算法的关键思想是 某一子串的hash值可以根据上一子串的hash在常数时间内计算出来，这样比对的时间复杂度可以降为O(n-k)。Rabin-Karp对字符串的hash算法和上面描述的一样（按整数进制解析再求模），假设原字符串为s，H(i)表示第i个字符开始的k个子字符串的hash值，即
，（先不考虑%M），则 ，时间为常数。

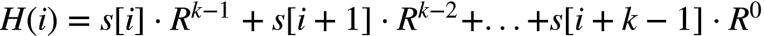
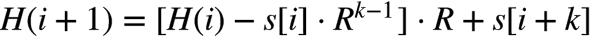
又由%的性质可得：

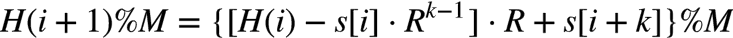
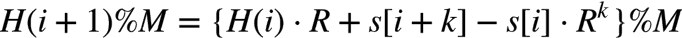
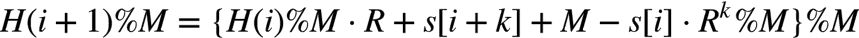
即 i+1 处子串的 hash 可以由 i 处子串的 hash 直接计算而得，在中间结果 %M 主要是为了防止溢出。

M 一般选取一个非常大的数字，子串的数目相对而言非常少，产生散列碰撞的概率为 1/M，可以忽略不计。

代码实现如下，这里当hash一致时没有再回退检查。可以看到 Rabin-Karp 的瓶颈在于每个内循环都进行了乘和模运算，模运算是比较耗时的，而其他算法大部分只需要进行字符比对：

package algorithm.string;

import java.math.BigInteger;

public class RabinKarp {

    private static long M = 1000000000000000003L;   //集合空间大小，一个很大的素数
    private static int R = 31;  //进制
    {
        //M = BigInteger.valueOf((long) Math.pow(10, 18)).nextProbablePrime().longValue();
    }

    private long patternHash;
    private long RK; // R^K % M，用于减去第一个数时的计算
    private int K; // 模式字符串的长度

    public RabinKarp(String pattern) {
        patternHash = hash(pattern);
        K = pattern.length();

        // 计算RM
        RK = 1;
        for (int i = 0; i < K; i++) {
            RK = (R * RK) % M;
        }
    }

    public int search(String txt) {
        long substrHash = hash(txt, 0, K);
        if (substrHash == patternHash) return 0;    //一开始就匹配成功
        for (int i = 1; i + K <= txt.length(); i++) {
            // H(i+1) % M = [H(i) % M * R + s[i+k] - s[i] * R^k % M + M] % M
            substrHash = (substrHash * R  + txt.charAt(i + K - 1) - txt.charAt(i - 1) * RK % M  + M ) % M;
            if (substrHash == patternHash)
                return i;
        }
        return -1;
    }

    // Horner rule 计算字符串hash值
    private long hash(String str, int start, int length) {
        long hash = 0;
        for (int i = start; i < length; i++) {
            hash = (hash * R + str.charAt(i)) % M;
        }
        return hash;
    }

    private long hash(String str) {
        return hash(str, 0, str.length());
    }

    public static void main(String[] args) {
        String pattern = "y similar t";
        RabinKarp rk = new RabinKarp(pattern);
        String txt = "Technically, this algorithm is only similar to the true number in a non-decimal";
        System.out.println(txt);
        int index = rk.search(txt);
        if (index >= 0) {
            for (int i = 0; i < index; i++) {
                System.out.print(" ");
            }
            System.out.print(pattern);
        }

    }
}

输出为：

Technically, this algorithm is only similar to the true number in a non-decimal
                                  y similar t

5. 二维扩展

Rabin-Karp 算法可以扩展到二维，可用于二维数组、图像的查找。基本思想如下：

问题：在一个 n1*n2 的二维字符组成中搜寻一个给定的 m1*m2 的模式。

首先来看模式矩阵。如果把m2列中的每一列都看做一个整体，那么他们每一个都是一个一维的串，可以分别计算出hash值（使用霍纳法则），这样模式矩阵就成了一个一维的长度为m2的模式串。

然后，对大矩阵的前m1行，用同样的方法能得到一个长度为n2的串。

这样，在大矩阵的前m1行中寻找模式矩阵，就转化成了一维的字符串匹配问题。（这里使用一维的串匹配算法就能解决，比如KMP）

最后，用同样的方法，在大矩阵的第2到第m1+1行，第3到m1+2行。。。都可以用同样的方法匹配。
这里的关键是，每次匹配时，转化后的一维串可以通过上次的串直接计算出来。（类似于Rabin-Karp由ts可以在常数时间内计算出ts+1）

可以想象成用一个m1*m2的窗口，在原矩阵上从左到右从上到下一格一格地比对。

在水平移动时，将窗口和窗口所在的m1行中（原矩阵）的所有列都hash成一个数字，这样问题就变成了一维的查找，可以用kmp之类的算法解决。

在垂直移动时，移动后窗口每列的hash值都能根据该列移动前的hash直接计算出来，Rabin-Karp一维时的规则此时依然适用。对于原矩阵也如法炮制，问题继续转换成一维的查找。

因此在实现时，使用两个一维数组，一个保存窗口中每列的hash，一个保存原矩阵每列（高度为窗口的高度）的hash，方便垂直移动时hash的重新计算。

代码TODO。

6. 参考资料

  1. 《Algorithms》
  2. S-Q Course Book
  3. Wiki
  4. 基础算法专题二：字符串匹配
  5. 关于同余与模运算的总结
  6. Rabin-Karp Method For Two Dimensional Arrays - Implementation in JAVA
  7. 二维模式（矩阵）匹配（Rabin-Karp算法推广到二维）
Loading Disqus comments...
目录