堆

1. 概述

堆是一个完全二叉树，其中每个节点的值都大于（或小于）其所有孩子节点的值，Top K 问题是堆的一个典型应用。

在很多地方又被称为 优先级队列，JDK 中的PriorityQueue就是基于堆实现的。

2. 实现

和其他完全二叉树一样，堆通常用一个数组实现，同时用一个变量记录当前堆内元素个数。

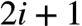
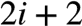
对元素 i，它的左孩子和右孩子分别为 ，，它的父节点为向下取整。

int[] heap;
int heapLength;

// helper funcs for parent/left child/right child fast access
Integer parent(int i){return (i-1)/2 >= 0 ? (i-1)/2 : null;}
Integer left(int i){return (2*i + 1) <= heapLength - 1? (2*i + 1) : null;}
Integer right(int i){return (2*i + 2) <= heapLength - 1? (2*i + 2) : null;}

堆常见的操作有：

1. init：用一个集合初始化堆
2. removeTop：删除堆顶
3. replaceTop：用一个元素代替堆顶，并返回原堆顶

堆也支持元素的增加、更新、删除等操作，但用的不多。

下面的讲解都是以小顶堆为例。

sink 和 float

sink和float是调整堆的两个核心动作。对于一个已经构造好了的对，当某个元素变大了，它需要往下下沉到合适的位置；反之则要上浮。

sink 的递归实现如下：

void sink(int i){
    Integer left = left(i),right = right(i);

    // 叶子节点，结束 sink 动作
    if(left == null && right == null) return;   

    // 如果只有左孩子且比它大，则交换二者的值，并继续 sink
    if(left != null && right == null && heap[i] > heap[left]) {
        swap(i,left);
        sink(left);
        return;
    }

    // 如果同时有左右孩子，则跟较小的孩子比较，如果比它大，则交换并继续 sink
    if(left != null && right != null){
        int min = heap[left] < heap[right] ? left:right;
        if(heap[i] > heap[min]){
            swap(i,min);
            sink(min);
        }
    }
}

float 的逻辑类似。

二者的时间复杂度都是 O(logN)。

init

从最后一个非叶子节点开始到根节点，依次对其调用sink()调整堆即可：

void initHeap(){
    for(int i = parent(heapLength - 1); i>=0 ; i--){
        sink(i);
    }
}

removeTop

用最后一个元素代替当前堆顶，并对其用sink()调整堆：

int removeTop(){
    int top = heap[0];
    heap[0] = heap[heapLength-1];
    heapLength -= 1;
    sink(0);
    return top;
}

replaceTop

用指定元素代替当前堆顶，再调用sink()：

int replaceTop(int n){
    int top = heap[0];
    heap[0] = n;
    sink(0);
    return top;
}

add

将元素加入数组最末，并用float()将其上浮到合适位置。

update

将新值和旧值比较，决定是用float()还是sink()调整堆。

delete

将堆的最后一个元素放到该位置，再通过float / sink调整堆。